Risikoorientierte Prüfungsplanung optimieren – Praxisnahe Umsetzung komplexer Bewertungslogiken in SQL

Um Anregungen für die Praxis zu geben, haben wir eine Logik in einem SQL-Server entwickelt, da Power Query bei den größeren Abfragen (8 Fragen mit 6 Antworten ergeben 1.679.616 Kombinationsmöglichkeiten) an Grenzen in der Performance stößt. Auch diesen Code können Sie bei Bedarf vollständig einsehen und in die eigene Umgebung laden.

Bei der Analyse sind wir immer von dem theoretischen Modell ausgegangen, dass ausschließlich qualitative Faktoren zur Messung benutzt werden. Sobald Sie operative Zahlen (vielleicht auch CPI-Werte von Transparency International, aber auch Umsatzzahlen, Geschäftszahlen der Teilbereiche, Investitionen) nicht in Form von Scores, sondern von echten Zahlenwerten einbinden, dürfte klar sein, dass sich das Bild komplett verändert. Aber auch hier muss der „nur“ qualitativ betrachtete Teil mit dem Einfluss auf das gesamte Modell einer Analyse unterzogen werden.

Wenn echte Zahlen eingebunden werden, wird das Bild spürbar objektiver und zugleich „skalensensitiv“; Vergleiche werden belastbarer, Backtesting wird möglich und damit die Qualität der Ableitung nachvollziehbar. Gleichzeitig lässt sich die Verarbeitung automatisieren. Die Kehrseite liegt auf der Hand: Einzelne Größen können das Gesamtbild dominieren; ohne saubere Normalisierung/Skalierung wird genau dieser Punkt zum modellkritischen Faktor. Zudem drohen Ausreißer, Volatilität und Periodeneffekte das Ergebnis zu verzerren. Und damit können Sie in der Regel nicht die Risiken über alle Prüfungsobjekte gleichermaßen messen (Personal, Compliance, Controlling als Beispiel).

Sobald qualitative Modelle gefahren werden, muss man sich zwischen ungewichteten und gewichteten Modellen entscheiden.

Die ungewichtete Variante wirkt in der Internen Revision oft „unparteiisch“ – sie fühlt sich fair an. Sie ist schnell erklärt, sauber auditierbar und robust gegen endlose Modell-Debatten. Es entsteht keine Scheingenauigkeit durch diskutierbare Gewichtszahlen, und die Versuchung, einzelne „High-Impact“-Indikatoren strategisch zu optimieren, ist deutlich geringer.

Sobald Gewichte ins Spiel kommen, kippt aber auch die Psychologie: Wer legt sie fest, nach welchen Regeln – und wie oft werden sie überprüft? Das ist ggf. diskutierbar und damit konfliktträchtig. Bleibt die Wirkung einzelner Gewichte intransparent, sinkt die Akzeptanz – selbst wenn das Modell rechnerisch „besser“ wäre. Transparenz und Begründung sind hier nicht Kür, sondern Pflicht.

Also sollten ungewichtete Modelle der gewichteten Methode vielleicht vorgezogen werden? Aus der Logik heraus können wir die Frage sehr schnell mit NEIN beantworten. Die Modelle mit einer Tiefe von 4 Fragen mit 3 Antworten bis hin zu 8 Fragen mit 8 Antworten haben wir alle durchgerechnet. Wenn man sich in der Internen Revision schon einmal gefragt hat, wieso so viele Prüfungen auf dem gleichen Termin landen – hier ist die Antwort:

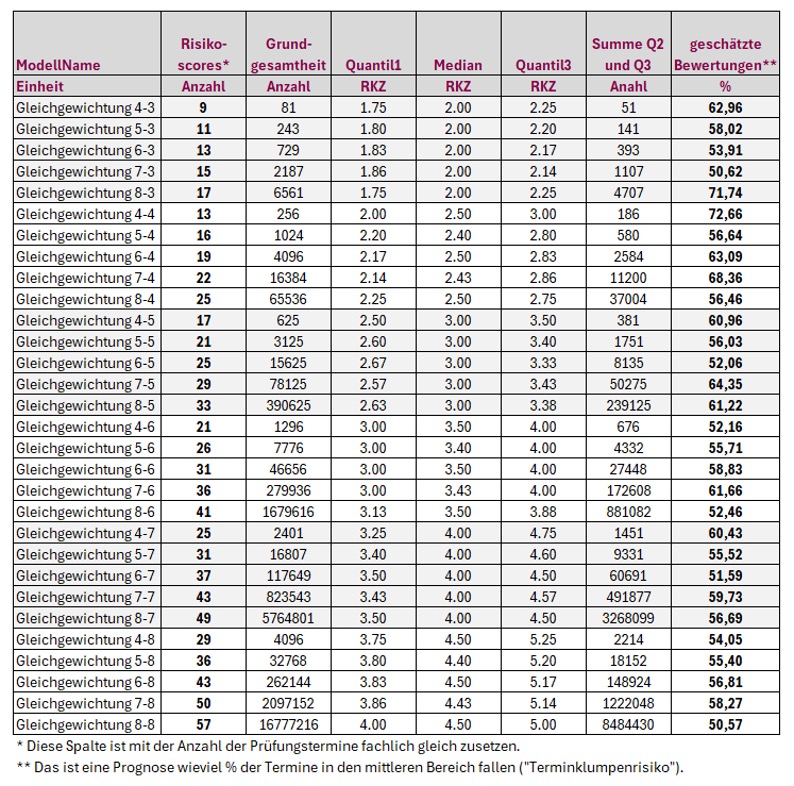
Egal wieviel Arbeit die Interne Revision in die korrekte Ermittlung der Risiken steckt, die maximale Trennschärfe beträgt 57 verschiedene Termine. Dann müssen sie allerdings auch die Kombinationen aus den jeweils niedrigsten und den höchsten Werten nutzen. Das dürfte allerdings vollkommen praxisfremd sein. Wenn die Bewertung eher zur Mitte tendiert, also sich in den mittleren von vier Quartilen abspielt, haben Sie in der letzten Spalte die zu erwartenden Werte auf Basis der Praxiseinschätzung (der Mensch tendiert zur Mitte – auch im Risikomanagement) stehen. Trennschärfe dürfte anders sein.

Mehr Aufwand mit mehr Fragen oder Antworten investieren? Definitiv nein – denken Sie immer an das Ziel – wir wollen nur nachweisen können, warum wir Prüfung A vor B gemacht haben. Und außerdem sprich die Mathematik dagegen – 10 Fragen mit 6 Antworten benötigen 6 hoch 10 Operationen in der Grundgesamtheit – das sind 60,5 Mio. Muster. Und wenn die logische Kette verfolgt wird – 21/26/31/36/41… dann wird auch ohne faktische Berechnung ein Wert um die 51 interpoliert ergeben. Dafür die Zahlenwüste erhöhen? NEIN, also benötigen wir andere Methoden.

Ergo müssen wir jetzt einmal Daten mit Gewichtungen, so sehr wir das auch dokumentieren müssen und die Skepsis in der Akzeptanz vorhanden ist, einmal beispielhaft durchrechnen. Um das Modell zu testen, haben wir bewusst 8 Fragen mit 6 Antworten ausgewählt, auch wenn dadurch erhebliche Rechenleistung verlangt wurde. Die getesteten Modelle haben wir mit nachvollziehbaren Namen beschrieben, so dass sie das eher erstaunliche Ergebnis nachvollziehen können:

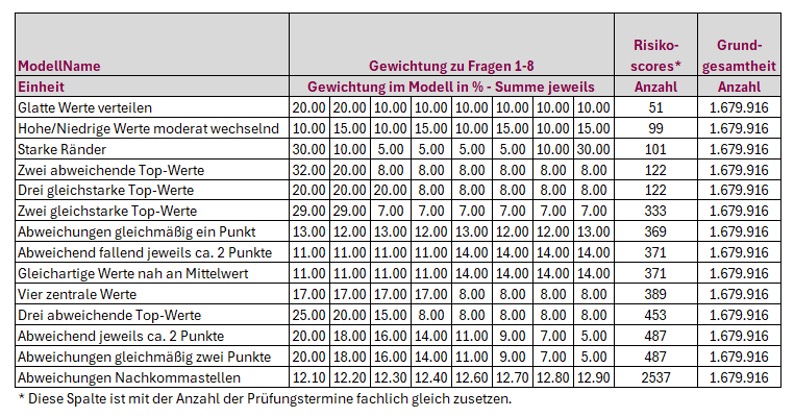
Die Tabelle ist aufsteigend nach Trennschärfe sortiert. Maßstab dafür ist die Spalte „Risikoscores – Anzahl“: Sie zählt, wie viele unterschiedliche Score-Ausprägungen ein Modell über die gesamte Grundgesamtheit erzeugt. Je höher die Zahl der unterschiedlichen Scores, desto feiner die Auflösung – und desto präziser lassen sich Prüfungstermine priorisieren.

Am unteren Ende stehen Modelle mit glatten, weitgehend gleichmäßigen Gewichten. Beispiel „Glatte Werte verteilen“: zwei Fragen mit 20 %, der Rest mit 10 %. Ergebnis: nur etwa 51 verschiedene Scores – dann kann man auch auf eine Gewichtung verzichten.

Auch Varianten wie „Hohe/Niedrige Werte moderat wechselnd“ oder „Starke Ränder“ — symmetrische Betonung der äußeren Fragen — kommen nur auf knapp dreistellige Werte (≈ 100). Diese Entwürfe sind gut erklärbar, aber sie verschenken Trennschärfe.

Sichtbar besser schneiden Modelle ab, die einzelne Fragen deutlich hervorheben. „Zwei abweichende Top-Werte“ und „Drei gleichstarke Top-Werte“ erhöhen die Varianz spürbar, die Anzahl unterschiedlicher Scores steigt in den mittleren dreistelligen Bereich. Der Mechanismus dahinter ist einfach: Unterschiedlich gewichtete Antworten erzeugen mehr kombinatorische Vielfalt in den Summen, Kollisionen (gleiche Gesamtsumme aus verschiedenen Antworten) nehmen ab. Dennoch bleiben es ganzzahlige Gewichte — und genau das begrenzt die Auflösung.

Interessant sind die „Mittelwert-Modelle“ wie „Gleichartige Werte nah am Mittelwert“ oder „Vier zentrale Werte“. Sie adressieren das Bauchgefühl, in der Mitte liege die Wahrheit. Technisch entsteht jedoch wieder viel Kompensation: Was die eine Frage gibt, nimmt die andere. Auch hier landen wir typischerweise bei rund 350–400 unterschiedlichen Scores — solide, aber noch keine echte Feinstruktur.

Die nächste Stufe sind feiner abgestufte Entwürfe: „Abweichungen gleichmäßig ein Punkt“, „… zwei Punkte“ oder „abweichend jeweils ca. zwei Punkte“. Die Idee: Statt großer Sprünge werden über alle Fragen kleine, systematische Differenzen eingeführt. Das reduziert Kollisionen weiter und hebt die Anzahl unterschiedlicher Scores deutlich an (oberer dreistelliger Bereich). Für die Praxis ist das bereits spürbar: Terminlisten werden weniger ‚blockig‘, Prioritäten zeichnen sich klarer ab.

Den entscheidenden Sprung bringt die letzte Zeile: „Abweichungen Nachkommastellen“. Hier werden die Gewichte nicht mehr nur ganzzahlig verteilt, sondern mit Dezimalstellen differenziert — beispielsweise 12,10 %, 12,30 % etc. Ergebnis: ein massiver Anstieg der unterschiedlichen Scores (in der Tabelle über 2.500). Warum? Ganzzahlige Gewichte führen zwangsläufig zu vielen arithmetischen Koinzidenzen: verschiedene Antwortmuster summieren sich auf denselben Wert. Nachkommastellen brechen diese Symmetrien auf. Lineare Kombinationen werden seltener identisch; die Rangfolge wird feinkörnig und stabil. Kurz: Nachkommastellen bringen die Lösung.

Was heißt das für die Modellwahl? Erstens: Die Spalte „Risikoscores“ sollte als harte Kennzahl für Trennschärfe verstanden werden — je höher, desto mehr unterscheidbare Prioritäten. Zweitens: Ein reines ‚gleichmäßig und glatt‘ ist psychologisch angenehm, schränkt aber die Präzision spürbar ein. Drittens: Wer interpretierbare Modelle möchte und dennoch trennscharf planen will, kombiniert moderate Schwerpunktsetzungen mit sorgfältig gewählten Dezimalstellen. Damit bleibt die Begründung anschlussfähig („Frage 1 und 8 sind etwas wichtiger“) und die Technik liefert zugleich eine klare, fein abgestufte Rangfolge.

Pragmatische Leitplanken: Gewichte weiterhin auf 100 % normieren; Dezimalstellen bewusst einsetzen (nicht inflationär, sondern gezielt, z. B. 0,1–0,3 %-Schritte bei ausgewählten Fragen); Symmetrien vermeiden (nicht alle Offsets identisch wählen); und die erreichte Trennschärfe regelmäßig prüfen. So entsteht ein Modell, das sowohl in Workshops erklärbar ist als auch im Tagesgeschäft liefert — mit genug Schärfe, um die wirklich wichtigen Fälle an die Spitze zu bringen.

Die erste Prozedur steuert die weitere Verarbeitung, sofern die Prozeduren alle geladen sind. Tabellen werden ebenfalls automatisiert erzeugt.

Die SQL Umsetzung folgt der im Artikel skizzierten Logik: Aus vorgegebenen Fragen‑/Antwortstrukturen werden vollständige Kombinationsräume gebildet, Scores (ggf. gewichtet) berechnet und zu aussagefähigen Aggregationen verdichtet. Ziel bleibt die prüfungspraktische Trennschärfe - nicht akademische Modellkomplexität.

Die Prozeduren wurden bewusst auf einem SQL-Server 2012 getestet, so dass diese ggf. auch auf älteren Installationen ebenso wie in der Cloud lauffähig sind. Ebenso ist es im Unternehmen vollständig legitim, die Daten in einen kostenfreien Server von Microsoft  - Produktname SQL EXPRESS -  zu integrieren.

Die Sammelprozedur dbo.pRiskModell_00_CompleteProcedures dient als „Ausführungsdatei“: Sie bereinigt ggf. alle Altdaten, sorgt für eine Logtabelle, durchläuft anschließend alle relevanten Prozeduren via Cursor und protokolliert Start/Ende, Laufzeit (mm:ss.mmm) und Return‑Codes in RiskModellLogfiles. Abschließend gibt sie die Laufstatistik zur schnellen technischen Qualitätssicherung aus.

Damit können Sie – vorausgesetzt Sie haben alle Prozeduren in den SQL-Server geladen – sich einfach zurücklehnen und die Modellergebnisse wie oben dargestellt in der Tabelle RiskModellInput anschauen. Wir haben die oben erwähnten Modelle alle bereits integriert und die Maschine benötigt auf einem handelsüblichen Notebook folgende Zeiten:

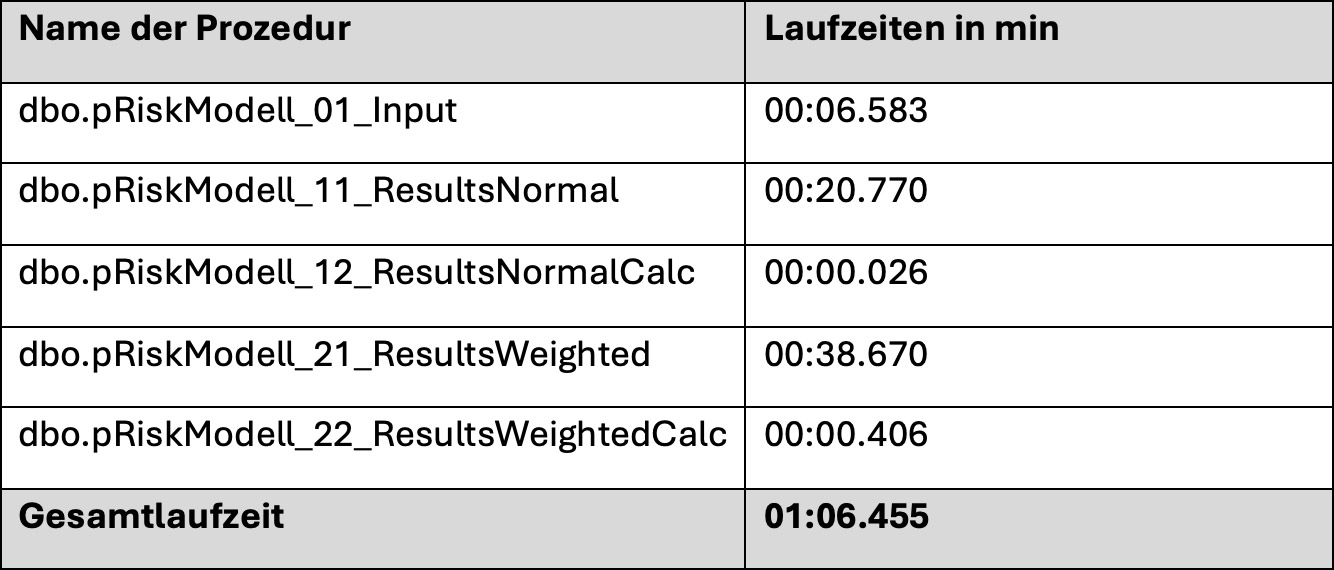
Der SQL-Ablauf wiederholt die im Artikel dargestellte Methodik in einer auditfesten, wiederholbaren Datenbankpipeline. Auf diese Weise lassen sich Modellparameter (Anzahl Fragen, Antworttiefen, Gewichtung) gezielt variieren und deren Einfluss auf die Trennschärfe belegen - eine wesentliche Voraussetzung für eine belastbare, risikoorientierte Prüfungsplanung.

Wir haben uns bewusst für eine Trennung nach ungewichteten und gewichteten Daten entschieden. Für das mehrfach eingesetzte Modell „8 Fragen und 6 Antworten mit Gewichtungen“ haben wir einmalig die rd. 1.7 Mio. Kombinationsmöglichkeiten materialisiert, um die Performance der Analyse zu erhöhen.

Die eigentliche Berechnung kann (ggf. nach einer Anpassung oder einer Integration von weiteren Modellen) jeweils über dbo.pRiskModell_99_Caller erneut angestoßen werden. Alle Abläufe sind im SQL-Code dokumentiert.